Graduate School Work
I received my Master of Science in Computer Science from the University of British Columbia in 2007. My research focused on mesh parameterization and developing systems for generating developable surfaces (surfaces realizable from a flat sheet) starting from arbitrary boundary curves.

Developable Surfaces from Arbitrary Sketched Boundaries (PDF)
This paper introduces an intuitive sketch-based approach for modeling developable surfaces. Developable surfaces are surfaces that can be unfolded into the plane without stretching or tearing, making them ideal for applications in manufacturing, architecture, and fashion design where materials come in flat sheets.
Our algorithm generates smooth discrete developable surfaces from user-specified 3D polyline boundaries, utilizing connections between developable surfaces and convex hulls. The approach allows designers to quickly prototype shapes that can actually be fabricated from sheet materials.
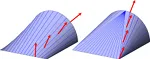
Modeling Developable Surfaces from Arbitrary Boundary Curves (PDF)
My thesis expands on the explanations presented in the conference paper and demonstrates additional applications of the developable surface generation algorithm. It provides a deeper theoretical foundation and explores the design space of developable surfaces more thoroughly.
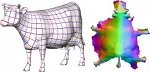
Mesh Parameterization Methods and their Applications (PDF)
This comprehensive survey covers methods for creating piecewise linear mappings between triangulations in 3D and simpler domains such as planar regions or spheres. Mesh parameterization is fundamental to many computer graphics applications including texture mapping, surface remeshing, and shape analysis.